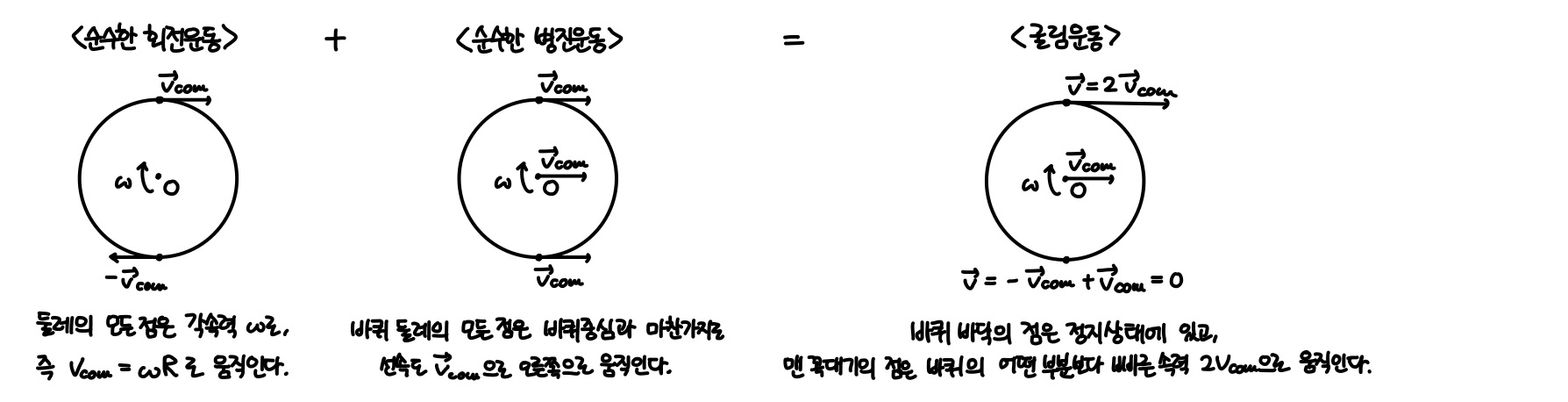
병진운동과 회전운동이 결합한 굴림운동

굴림운동에서 물체의 질량중심 O는 일정한 속력 Vcom으로 앞을 향하여 움직인다.

원호 s와 회전각도 θ 사이의 관계는 s=θR을 만족한다.
식을 시간에 대해 미분하면 병진운동의 속도 Vcom=ωR을 얻을 수 있다.
다시 한번 식을 시간에 대해 미분하면 병진운동의 가속도 a=αR을 얻을 수 있다.

물체가 구름 운동을 하기 위해서는 마찰이 필요하다(마찰 없이는 미끄러지지 않으며 구르는 것이 불가능하다).
하지만 물체가 완전히 구르는 운동을 시작하게 되면 접촉점의 속도가 0이므로 마찰력은 더 이상 일을 하지 못하고 따라서 역학 에너지가 보존된다(에너지의 손실이 없다).

힘과 굴림운동의 운동에너지

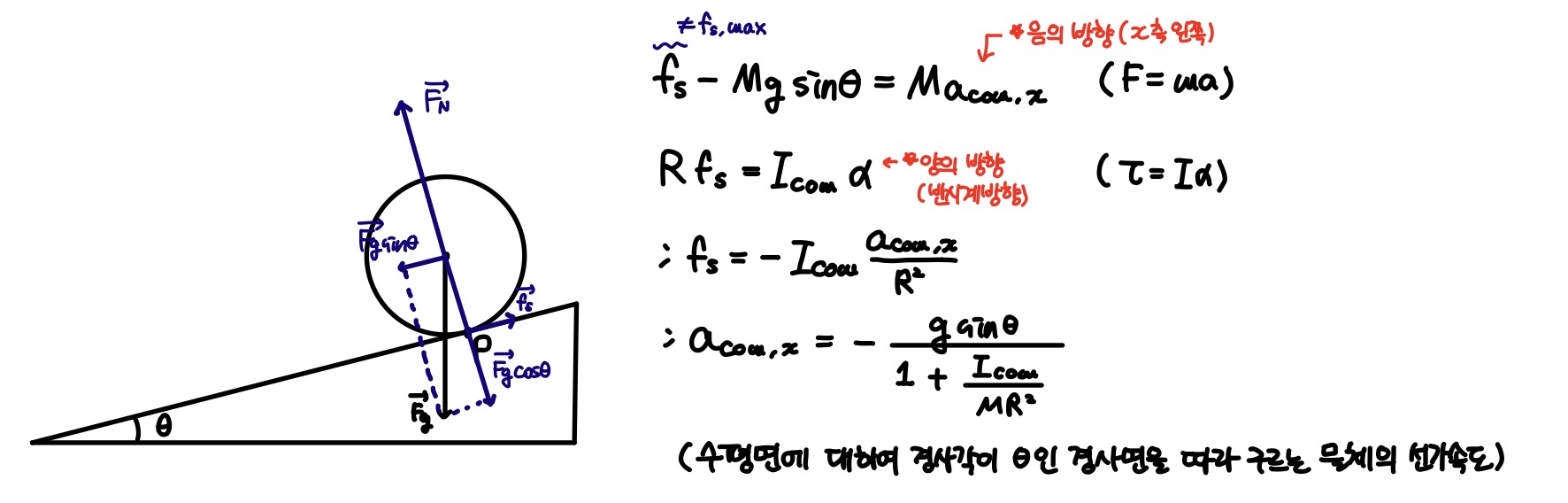
바퀴가 일정한 속도로 구른다면 접촉점에서 바퀴가 미끄러지려고 하지 않으므로 바퀴에 작용하는 마찰력이 없다.
그러나 알짜힘이 바퀴에 작용하여 바퀴중심의 속력을 증가 또는 감소시킨다면 질량중심은 가속도 acom의 방향으로 가속된다.
이 힘은 바퀴의 회전을 빠르거나 느리게 하므로 각가속도 α가 발생한다.
이러한 가속도 때문에 접촉점에서 바퀴가 미끄러지려는 경향이 나타나고, 이를 억제하려는 마찰력이 바퀴에 작용한다.

만약 바퀴가 미끄러지지 않는다면 이 힘은 정지마찰력 fs이고 바퀴는 유연하게 구르게 된다.
알짜힘이 작용할 때 바퀴가 미끄러진다면 접촉점에 작용하는 마찰력은 운동마찰력 fk이고 이때는 식 a=αR을 적용할 수 없다.

바퀴의 회전이 빨라지면 바퀴의 밑바닥이 접촉점에서 왼쪽으로 미끄러지려 한다.
접촉점에서의 마찰력은 바퀴가 미끄러지지 않게 하려고 접촉점에서 오른쪽으로 바퀴에 작용한다.
바퀴가 미끄러지지 않는다면 마찰력은 정지마찰력 fs가 된다.
바퀴의 회전이 느려지는 경우에는 질량중심의 가속도 acom과 마찰력 fs는 왼쪽을 향한다.

경사면을 내려오는 굴림운동

요요

요요를 거리 h만큼 풀어서 굴러 내리게 하면 mgh만큼의 퍼텐셜에너지를 잃는 대신 병진운동에너지(1/2mv^2)와 회전운동에너지(1/2Iω^2)를 얻는다. 요요가 튀어 올라올 때는 운동에너지를 잃고 퍼텐셜에너지를 다시 얻는다.

끈을 축 둘레에 감는 요요의 경우에는, 요요가 끈의 끝에 다다랐을 때 끈이 위쪽으로 축에 가하는 힘에 의해 병진운동을 멈추고 단지 회전운동에너지만 가지고 고리 안쪽에서 자전하게 된다.

다시 살펴본 토크

토크의 정의를 일반화시켜 고정된 점에 대하여 운동하는 입자에 적용해 보자.
이때 입자의 경로는 그 점에 대하여 원일 필요는 없으며, 토크는 임의 방향을 가지는 벡터 τ로 표기한다.

각운동량

회전운동에 관한 Newton의 제2법칙

강체의 각운동량

고정축에 대해 회전하는 강체에 대해, 회전축에 평행한 각운동량 성분은 다음과 같다.
L=Iω (I: 고정축에 대한 강체의 회전관성)

각운동량 보존