회전변수
물체가 직선이나 곡선을 따라 움직이는 병진운동 vs 어떤 축을 중심으로 회전하는 회전운동 (새로운 물리량 도입 필요)
힘 vs 토크
질량 vs 회전관성
강체: 구성요소가 고정되어 있어서 모양이 전혀 변하지 않으면서 회전할 수 있는 물체
고정축(회전축): 회전운동을 하는 동안 움직이지 않는 축
기준선: 회전축과 수직하게 임의로 정한다. 물체에 고정되어 물체와 함께 회전한다.
순수한 회전운동(각운동)에서는 물체의 점들이 각각의 중심이 회전축 위에 있는 원을 따라 움직이고, 각 점이 특정한 시간간격 동안 이동하는 각도가 같다.
고정된 방향에 대해 기준선의 각위치 θ를 라디안으로 측정;
θ=s/r (s는 x축에서 기준선까지의 원호 길이, r은 원호 반지름)
병진운동에서 물체의 위치를 시간의 함수 x(t)로 알고 있다면 물체의 운동에 대해 모든 것을 알 수 있듯이, 회전운동에서 기준선의 각위치를 시간의 함수 θ(t)로 안다면 회전하는 물체에 대한 모든 정보를 알 수 있다.
각변위 Δθ=θ2-θ1
반시계방향의 각변위는 양의 값, 시계방향의 각변위는 음의 값을 갖는다.

입자가 직선 위에서만 움직이도록 제한하면 입자의 위치나 속도, 가속도를 나타낼 때 굳이 벡터를 사용할 필요가 없다. 움직이는 방향이 두 방향뿐이므로 각 방향을 양수와 음수로 표시하면 되기 때문이다. 마찬가지로 어떤 축을 중심으로 회전하는 강체도 축을 따라서 시계방향이나 반시계방향의 회전만 있을 뿐이다. 따라서 각각의 방향을 양수와 음수로 나타낼 수 있다.
등각가속도 회전
병진운동에서 등가속도 직선운동이 중요했듯이, 회전운동에서는 등각가속도 운동이 중요하다. 이 경우에도 등가속도 직선운동에 대응하는 일련의 방정식들이 성립한다. 병진운동 방정식에 있는 선변수들에 대응하는 각변수들로 바꾸어 방정식을 간단히 얻을 수 있다.
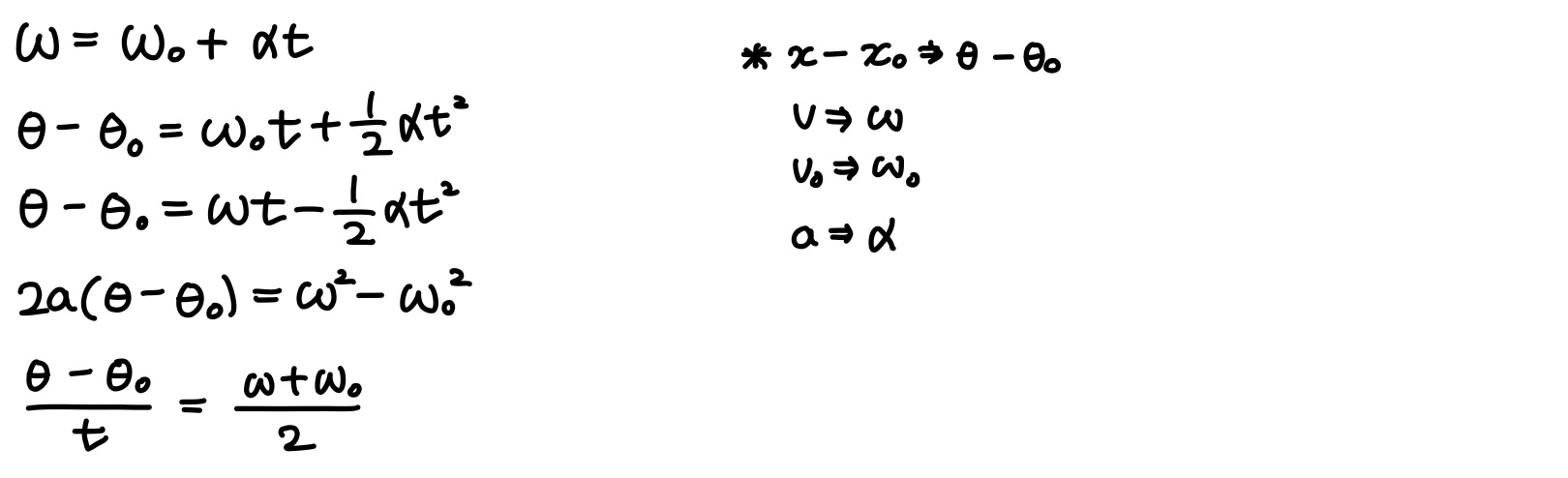
선변수와 각변수의 관계
회전운동을 다룰 때는 회전체의 특정한 점에 대해 선변수 s, v, a와 각변수 θ, ω, α사이의 관계를 알아야 한다. 이 관계는 회전축에서 그 점까지의 수직거리 r(회전축 주위로 그 점이 돌게 되는 원의 반지름 r과 같음)을 도입하여 구할 수 있다.

두 번째 식을 통해 강체 내 모든 입자의 각속력 ω은 같지만 선속력 v는 반지름이 큰 입자일수록 크다는 것을 알 수 있다.
가속도는 항상 지름성분이 있고, 경우에 따라 접선성분도 있다(각가속도가 0이 아닐 때).
회전 운동에너지
회전강체는 서로 다른 속력으로 움직이는 입자들의 결합체로 취급할 수 있다. 즉, 이들 입자의 운동에너지를 합하면 물체 전체의 운동에너지를 구할 수 있을 것이다.
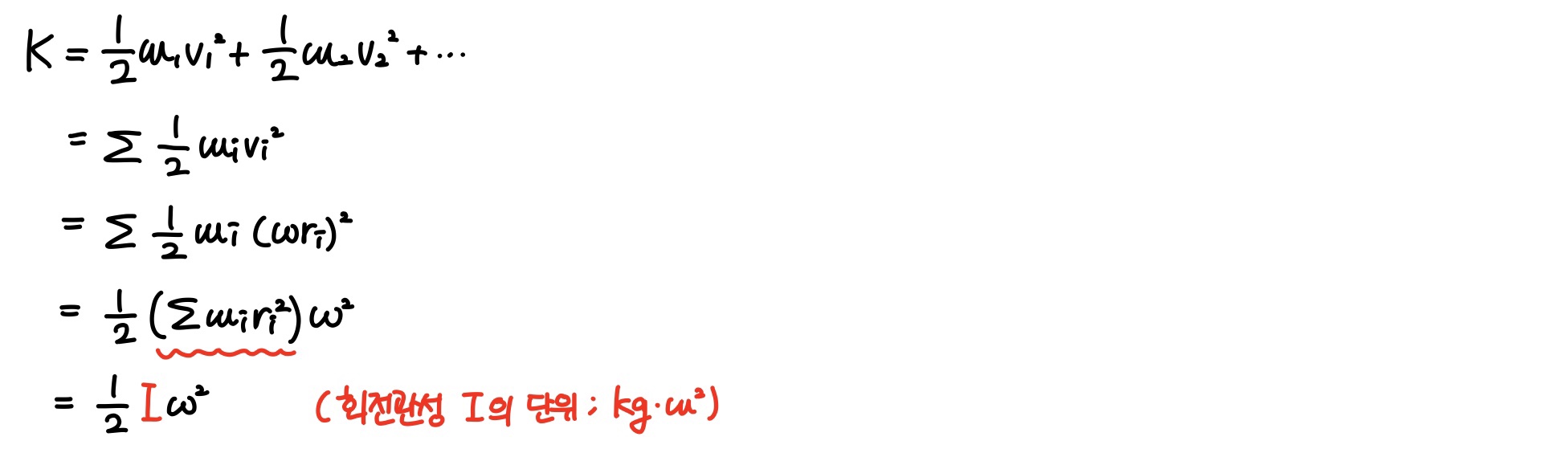
회전관성 계산하기

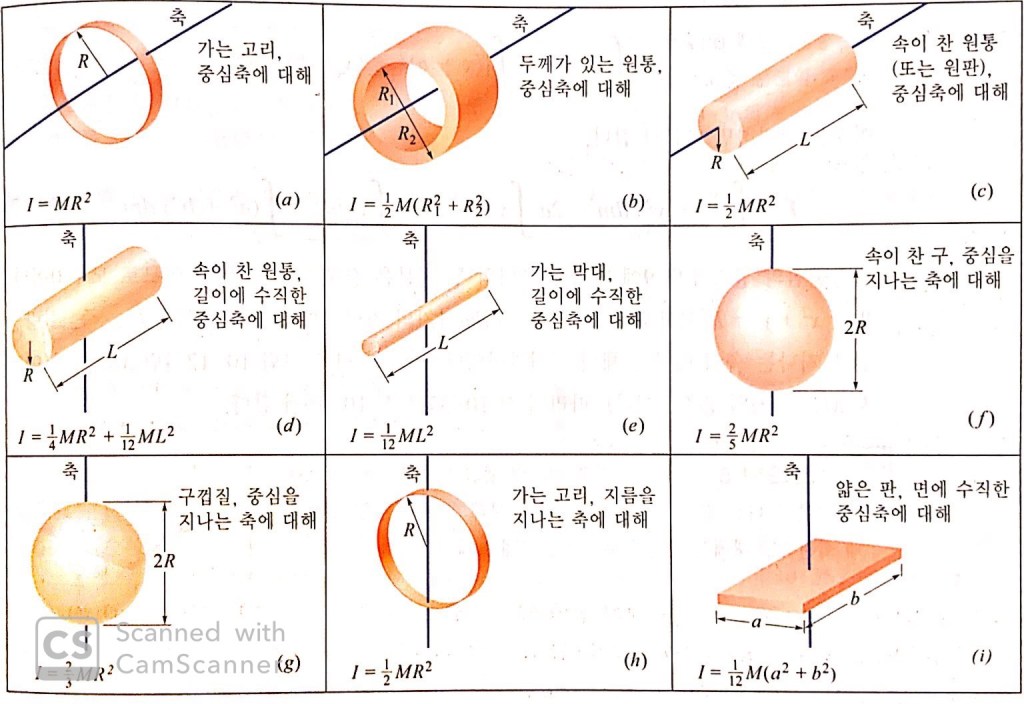
출처: 일반물리학 개정10판(David Halliday), 표 10-2

토크
토크는 힘 F에 의해 회전축 주위로 물체를 돌거나 비틀게 하는 작용이다.
힘 F가 축에 대해 위치벡터 r 떨어진 점에 작용하면 토크의 크기는 다음과 같다.

회전에 관한 Newton의 제2법칙

일과 회전 운동에너지
