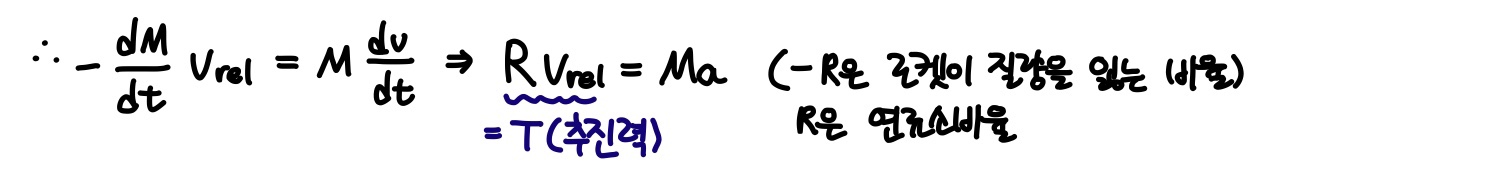질량중심

물체나 물체들로 이루어진 계의 질량중심은

1. 모든 질량이 그 점에 모여 있고
2. 외부력이 모두 그 점에 작용하는 것처럼 움직이는 특별한 점이다.

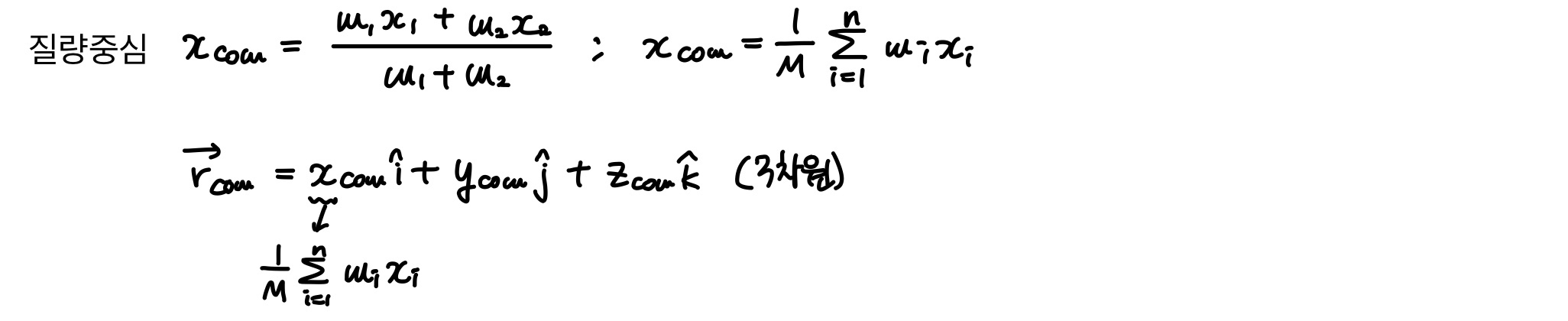
입자계에 대한 Newton의 제2법칙

선운동량

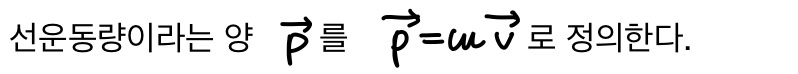
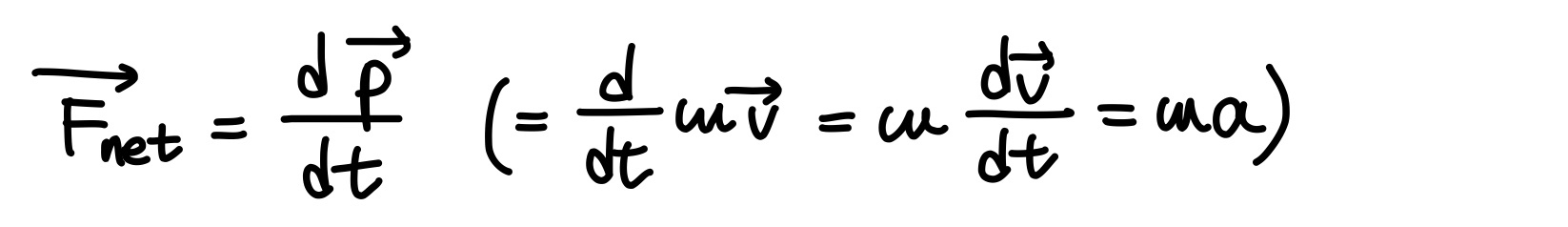
입자계의 선운동량은 계의 총질량 M과 질량중심의 속도를 곱한 것과 같다.

충돌과 충격량

충돌에서 외부력은 물체에 아주 짧은 시간 동안 매우 큰 크기로 작용하여 물체의 운동량을 변화시킨다.

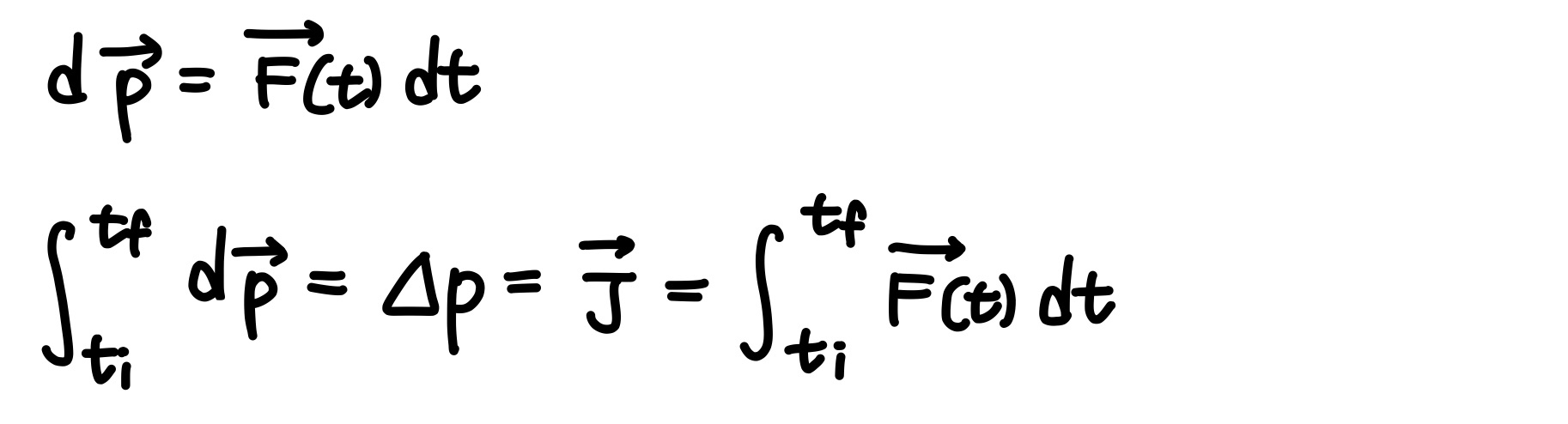
선운동량의 보존

입자계에 알짜 외부력이 작용하지 않으면 계의 전체 선운동량 P는 변하지 않는다.
Pi=Pf

충돌의 선운동량과 운동에너지

충돌에 의해 전체 운동에너지가 변하지 않는다면 운동에너지가 보존되고, 그러한 충돌을 탄성충돌이라 한다.
운동에너지의 일부가 다른 형태의 에너지로 빠져나가며 보존되지 않는 충돌을 비탄성충돌이라 한다.
두 물체의 비탄성충돌에서는 항상 계의 운동에너지를 잃어버린다. 가장 큰 손실은 두 물체가 서로 붙어버릴 때 생기는데 이런 충돌을 완전 비탄성충돌이라고 한다.

물체의 비탄성충돌에서 입자계의 운동에너지는 보존되지 않지만, 계가 닫힌 고립계일 경우 계의 전체 선운동량은 반드시 보존된다.

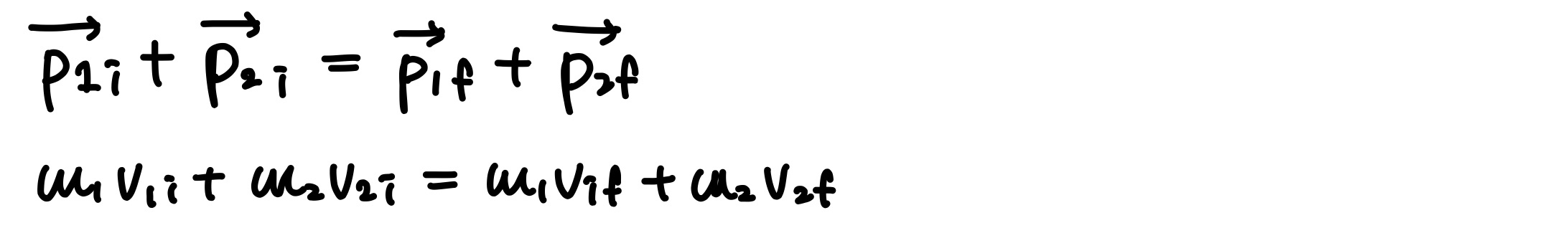
두 물체의 완전 비탄성충돌에서 질량 m2의 물체가 처음에 정지해 있고(표적) 질량 m1의 물체가 다가와(포물체), 충돌 후 두 물체가 붙어 V의 속력으로 함께 움직인다면

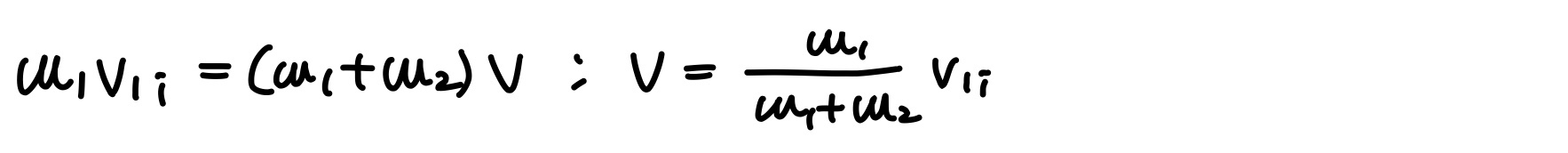
1차원 탄성충돌

탄성충돌에서 충돌과 관련된 각 물체의 운동에너지는 변할 수 있으나 계의 전체 운동에너지는 변하지 않는다.

1. 동일 질량(m1=m2)
   v1f=0, v2f=v1i (움직이던 물체는 충돌한 자리에서 멈추고, 표적은 자신을 때린 물체와 같은 속도로 움직이기 시작한다. 즉, 서로의 속도를 바꿔 가진다.)
2. 질량이 큰 표적(m2>>m1)
   v1f≈-v1i, v2f≈(2m1/m2)v1i (들어온 물체는 충돌 전과 거의 같은 속도로 뒤로 튕겨 나오고, 표적은 매우 작은 속도로 천천히 앞으로 움직인다.)
3. 질량이 큰 포물체(m1>>m2)
   v1f≈v1i, v2f≈2v1i (들어온 물체는 충돌 후에도 원래의 속도로 움직이고, 표적은 자신을 때린 물체의 두 배의 속도로 앞으로 움직인다.)

2차원 충돌

두 물체가 충돌하면서 단일 축 위에 있지 않으면(정면충돌이 아니면) 이 충돌은 2차원 충돌이다.

닫힌 고립계에서 운동량 보존법칙을 적용하고, 충돌이 탄성충돌이라면 운동에너지 보존법칙을 사용한다.

질량이 변하는 계: 로켓

로켓과 같이 가속되면서 질량이 변하는 경우, Newton의 제2법칙을 로켓뿐만 아니라 로켓과 연소되어 배출되는 물체 전체에 적용하여 다룰 수 있다. 전체 계의 질량은 로켓이 가속되더라도 변하지 않는다.

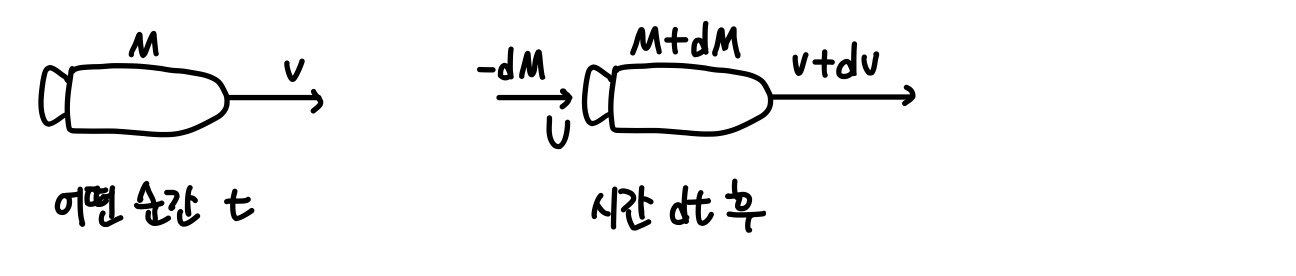
계가 닫힌 고립계이므로 dt 시간 동안 선운동량은 보존된다(Pi=Pf).
즉, Mv = (-dm)(U) + (M+dM)(v+dv) 이다.

로켓과 배기물 사이의 상대속력 Vrel을 사용하면,
(기준틀에서 본 로켓의 속도) = (배기물에 대한 로켓의 상대속도) + (기준틀에서 본 배기물의 속도) 이므로
(v+dv) = Vrel + U
U를 위의 식에 대입하여 정리하면
(-dM)(Vrel) = (M)(dv)