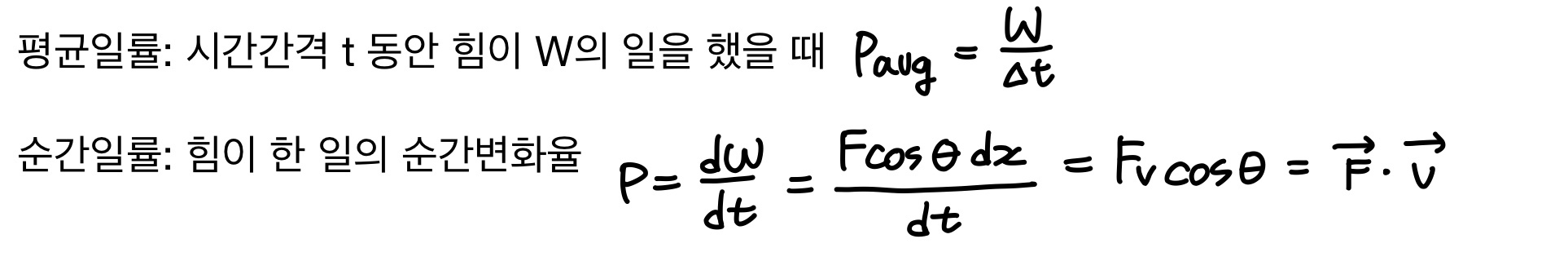운동에너지

질량 m인 물체의 속력 v가 광속보다 훨씬 작을 때, 운동에너지를 다음과 같이 정의한다.
K=1/2mv^2

운동에너지의 SI 단위 = 줄(J)
1J = 1kg*m^2/s^2 = 1N∙m

일과 운동에너지

일 W는 물체에 작용하는 힘을 통해서 물체로부터 혹은 물체로 전달되는 에너지다.
따라서 ‘일’은 전달된 에너지이고, ‘일을 한다는 것’은 에너지를 전달하는 행위이다.
일은 에너지와 같은 단위를 갖는 스칼라량이다.

변위 d동안 일정한 힘 F가 작용하는 입자에 가한 일은
W=Fdcosθ=F∙d (벡터의 스칼라곱)

이동하는 동안 힘이 물체에 한 일을 계산할 때 힘의 변위방향 성분만 사용한다. 변위방향에 수직한 힘의 성분이 한 일은 0이다.
힘에서 변위와 같은 방향의 벡터성분은 양의 일을 하고, 반대방향의 벡터성분은 음의 일을 한다.

알짜일은 각 힘이 한 일의 합이다.
(1) 각 힘이 한 일을 더하여 얻을 수 있다.
(2) 알짜힘 Fnet을 먼저 구한 다음에 Fnet의 크기 F와 두 벡터 Fnet과 d의 사이각을 구해서 얻을 수 있다.

일-운동에너지 정리

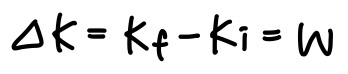
중력이 한 일

W=Fdcosθ 에서 F 대신 중력의 크기 mg를 사용하면 중력이 한 일 Wg는 다음과 같다.

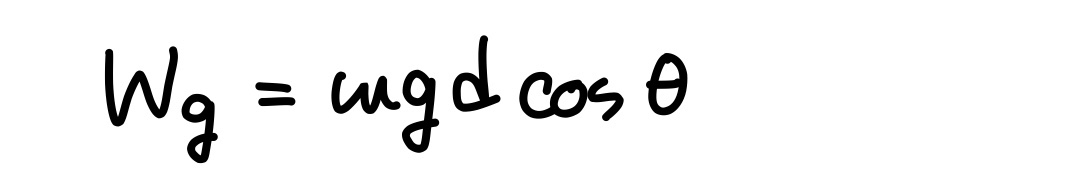
물체를 수직방향으로 들어올릴 때 외부력은 물체에 양의 일 Wa를 전달하는 반면에 중력은 물체에 음의 일 Wg를 한다(중력은 물체에서 외부로 에너지를 전달한다).

두 에너지 전달에 따른 물체의 운동에너지 변화량은 다음과 같다.

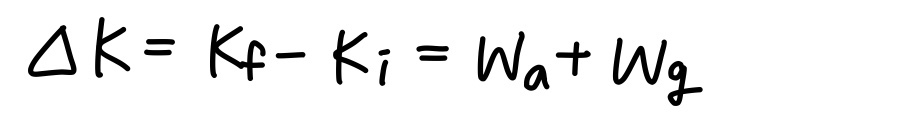
용수철 힘이 한 일

용수철에는 용수철을 평형상태로 복귀시키려는 용수철 힘이 작용한다(복원력).
용수철 힘 Fs는 다음과 같다.

x축을 용수철의 길이방향과 평행하게 잡고, 평행위치를 원점으로 잡으면 다음과 같이 식을 바꿔 쓸 수 있다.

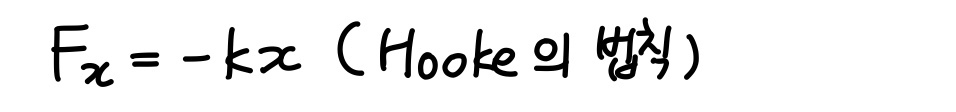
용수철 힘은 용수철 한 끝의 변위에 따라 변하는 힘이다(x의 함수꼴이다).

이러한 식을 통해 답을 구할 때에는, (1) 용수철의 질량은 없고, (2) 용수철은 이상적인 용수철이라는 조건이 적용되어 있다.

용수철 힘이 물체에 한 일을 구할 때에는 Fdcosθ 대신 미적분을 통해 얻은 식을 사용한다(힘이 한 값만을 가지지 않고 변하기 때문이다).

토막의 최종위치가 초기위치에 비해서 평형위치 x=0에 더 가까이 있다면 용수철이 한 일 Ws는 양의 값이다. 토막의 최종위치가 초기위치에 비해서 평형위치 x=0에서 더 멀리 떨어져 있다면 Ws는 음의 값이다. 최종위치와 초기위치가 평형위치 x=0에서 같은 거리에 있다면 한 일은 0이다.

만약 xi=0이고 최종위치를 x라고 하면 용수철 힘이 한 일을 다음과 같이 표기할 수 있다.

변하는 힘이 한 일

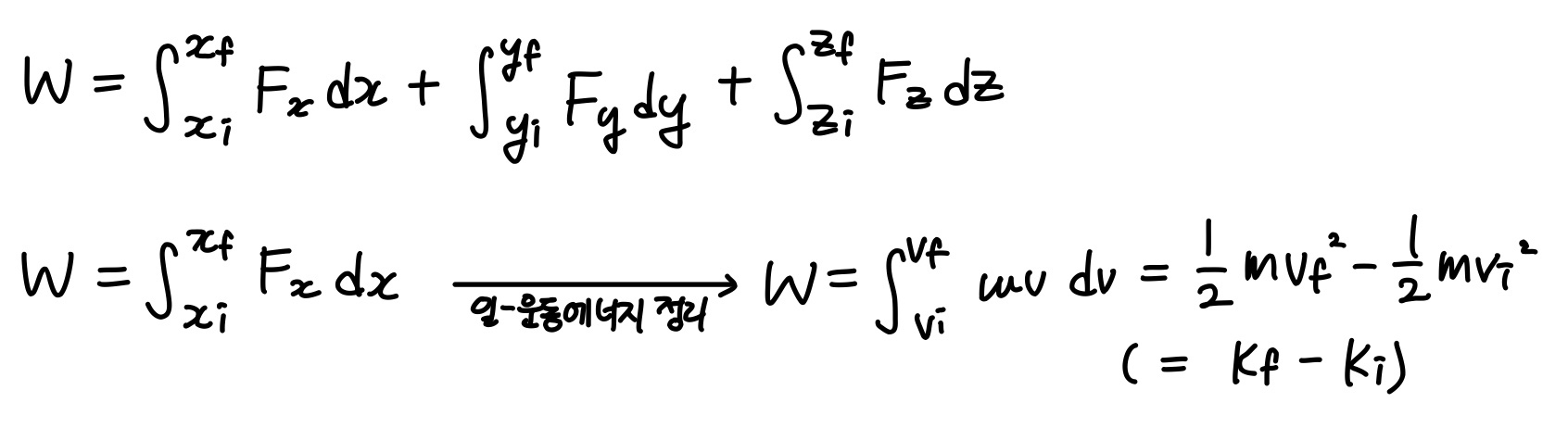
일률

일률: 힘이 한 일의 시간변화율 (단위: W)

1kw∙h = (10^3W)(3600s) = 360000J