철학

[기호논리학] 서장 – 연습문제

eunhyeong댓글 남기기

1. 필연적 참 / 우연적 참 / 거짓으로 구분, 필연적 참이라면 논리적 참인가 그렇지 않은가, 애매성 혹은 모호성이 결정적인 것들로 보이는 경우

  • 서울시의 인구는 10만명이 넘는다. – 우연적 참
  • 어떤 콘서트 피아노 연주자들은 프랑스인이다. – 우연적 참
  • 모든 검은 개는 개이다. – 필연적 참, 논리적 참은 아니다.
    • 모든 가짜 돈은 돈이다.
  • 모든 범죄 혐의자는 범죄자이다. – 거짓
  • 모든 범죄 혐의자는 혐의를 받고 있다. – 필연적 참, 논리적 참은 아니다. (모든 A인 B는 C이다.)
  • 모든 까마귀는 검다. – 거짓
  • 만일 두 사람이 형제간이라면 그들은 형제간이거나 자매간이다. – 필연적 참, 논리적 참
  • 만일 한 사람이 다른 사람보다 키가 크다면 후자는 전자보다 키가 작다. – 필연적 참, 논리적 참은 아니다.
    • 만일 한 사람이 다른 사람보다 귀엽다면 후자는 전자보다 예쁘다.
  • 올라가는 것은 무엇이든지 내려가야 한다. – 모호하다. ‘올라간다’, ‘내려간다’
  • 두 물체는 동시에 동일한 장소에 있을 수 없다. – 모호하다. ‘물체’
  • 한국어로 ‘영국’은 영국을 지칭한다. – 우연적 참
  • 모든 양의 정수 x, y, z에 대해서 만일 x<y이면 x+z<y+z이다. – 필연적 참. 논리적 참은 아니다.
    • 모든 정수 x, y, z에 대해서 만일 x<y이면 x*z<y*z이다.

2. (생략)

3. (만일 가능하다면) 다음 조건을 만족하는 예를 하나 드시오

  • 모든 대입예가 필연적 참인 문장틀; A는 B이거나 B가 아니다.
  • 약간의 대입예들은 필연적 참이고 약간의 대입예들은 그렇지 않은 문장틀; 모든 A는 B이다.
    • ‘모든 대입예가 필연적 참인 문장틀’, ‘어떠한 대입예도 필연적 참이 아닌 문장틀’ 두 특수한 경우를 제외하고 대부분의 문장틀이 여기에 속하는 것으로 보인다.
  • 어떠한 대입예도 필연적 참이 아닌 문장틀; A는 A가 아니다.
  • 첫번째 문장틀의 모든 대입예가 두번째 문장틀의 대입예이지만 그 역은 성립하지 않는 한 쌍의 문장틀; ‘S이거나 S가 아니다’, ‘S이거나 T가 아니다’
  • 참인 전제들과 거짓인 결론을 갖는 타당한 논변; 불가능하다(타당한 논변의 정의).
  • ‘2+2=4’를 결론으로 가지는 부당한 논변; 불가능하다(필연적 참이 결론인 논변은 부당할 수 없다)
  • 하나의 거짓 전제, 하나의 참 전제, 그리고 참인 결론을 갖는 타당한 논변과 부당한 논변; 내 평점은 4보다 낮다. 평점이 4 이상인 모든 사람은 장학금을 받는다. 그러므로 나는 장학금을 받지 못한다. (타당한 논변) 뭐가 참이고 뭐가 거짓인지는 ^^.. ; 어떤 한국인은 죽는다. 모든 기린은 불멸한다. 따라서 어떤 한국인도 기린이 아니다. (부당한 논변)

4. 다음의 일반화들 중 옳은 것은? (쉬운 문제는 생략함)

  • 모든 임의의 세 문장 R, S, T에 대해, 만일 R이 S와 T로부터 따라나오면 not T는 S와 not R로부터 따라나온다; O
  • 모든 임의의 세 문장 R, S, T에 대해, 만일 R이 S로부터 따라나오고 또한 not S로부터도 따라나오면 R은 T로부터 따라나온다; O (R은 필연적으로 참인 문장)
  • 모든 임의의 세 문장 R, S, T에 대해, 만일 R이 S와 T로부터 따라나오면 그러면 If S then R이 T만으로부터 따라나온다; O

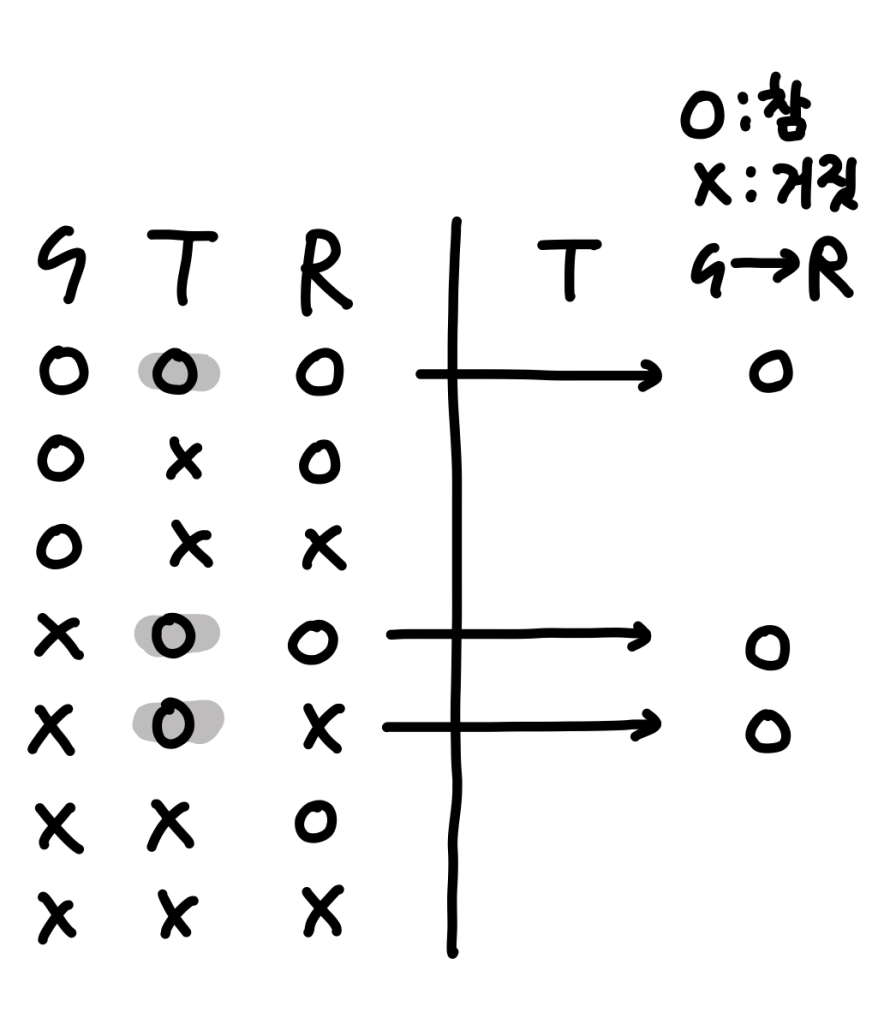
첫 번째, 두 번째 문제는 사실 흔히 아는 명제와 대우명제를 사용하면 쉽게 풀 수 있다. 그러나 출제 의도는 ‘따라나온다(=귀결이다 =논변이 타당하다)’를 ‘논변이 타당하다’의 정의인 ‘전제가 참일 때 결론이 거짓인 경우가 존재하지 않는다’로 푸는 것이다. 따라서 세 번째 문제를 풀기 위해서는 먼저 R이 S와 T로부터 따라나온다는 전제를 사용하여 S와 T가 모두 참일 때 R이 거짓인 경우 하나를 제외한 7가지 경우를 얻어야 한다. 그리고 7가지 경우 중 T가 참인 3가지 경우에서 If S then R이 거짓인 경우가 없는지 살핀다. 위 문제에서는 그런 경우가 없기 때문에 If S then R이 T에서 따라나온다고 말할 수 있다. 첫 번째와 두 번째 문제도 이러한 방식으로 해결할 수 있다.

* 개인적으로 어려웠던 문제는 볼드체로, 개인적인 생각을 덧붙여 서술한 것은 밑줄로 표시하였다. 또한 답안 중 틀린 것이 있을 수 있음을 밝힌다.

댓글 남기기